MSM-CanProg (UK)

Overview

The MSM-CanProg (UK) model comprises two main components: a continuous-time, non-homogeneous multistate model (MSM) to estimate natural history parameters, and a microsimulation based on the MSM framework to evaluate screening and active surveillance schedules, with the aim of optimizing the benefit-harm trade-offs of screening and active surveillance.

1. The MSM comprises three subcomponents:

   • Natural history component (See Figure 1 - blue arrows)
   • Progression of disease from clinical diagnosis to death (see Figure 1 - red arrows)
   • Progression of disease from screen-detection to death (See Figure 2)

   We have expanded our MSM to include seven states: 'healthy'/no-detectable cancer (S1), early screen-detectable (S2), late screen-detectable (S3), early screen-detected (S2-b), late screen-detected (S3-b), early clinically diagnosed (S4), late clinically diagnosed (S5), death from other causes (S6), and cancer-specific death (S7). The early state is defined as a tumor with a Gleason score <7 and the late state as a Gleason score ≥ 7.

   The transition from preclinical to clinical state is interval censored, while the transitions to clinical states and death occur at exact times, with death from other causes as competing risk on transitions from healthy to preclinical and preclinical to clinical states. The first observation in non-screened individuals is considered left censored. All individuals are assumed to be truly in state S1 at some initial age. In modelling the natural history of prostate cancer, age 40 is used as the left truncation age. An individual with negative screening test result may truly be in state S1 or could be in state S2 or S3 and misclassified as being in state S1.

   With our MSM, we can estimate the transition hazards between states, sensitivity of the screening episode (1- probability of misclassification), and derive the sojourn time, the length of time spent in preclinical state given that an individual transitions to clinical state.

   Our MSM can be extended to incorporate intermediate states occurring between screen-detection or clinical diagnosis and death.

   

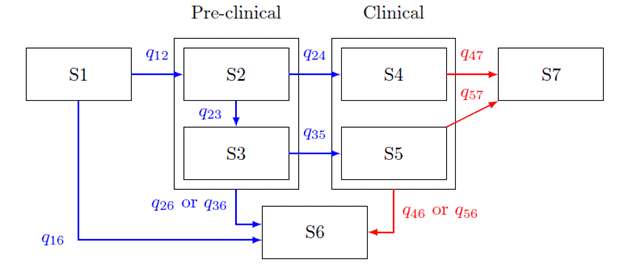
   Figure 1: The state transition diagram for the natural history model including the progression of disease from clinical diagnosis to death, where q_ij is the transition hazard from State i to j.

   

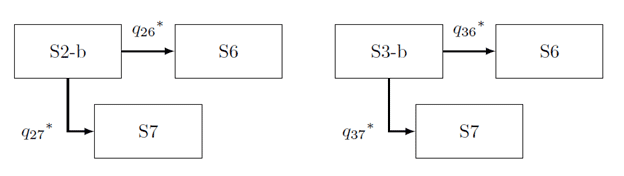
   Figure 2: The state transition diagrams from the screen detection to death, where q_ij^* is the transition hazard from State i to j.

   The key feature of our MSM:

   • It allows using interval censored, left censored, right censored, and left truncated panel data
   • Data can be used from both screened and unscreened population to derive transition parameters
   • Each transition can be specified by a variety of parametric models including exponential, Weibull, and Gompertz hazard models
   • With a parametric approach, the model can be used for prediction and out-of-sample extrapolation
   • Age varying transition hazards and age-varying misclassification are estimated simultaneously
   • The transition parameters are estimated by optimisation process to maximise the likelihood function built from the transition intensity function

2. The microsimulation is based on the MSM framework and has three subcomponents:

   • Projection of individual life trajectories from birth to death
   • An embedded natural history component
   • Overlaid screening or active surveillance processes

   The key features of our microsimulation:

   • A flexible simulation scheme that allows superimposing different screening strategies by varying calendar years, age range, frequency, and uptake of screening
   • Transition parameters and misclassification probabilities derived from MSM are used as input parameters
   • Allows projection and comparison of outcomes across different screening strategies or active surveillance schedules, such as screen-detected cancers, interval cancers, overdiagnoses, and cancer-specific deaths
   • When panel data are not available, the microsimulation can be used to derive the transition parameters from aggregate data, with outputs calibrated against observed outcomes. Then a multistate model is fitted to the simulated data to estimate the transition parameters and misclassification
   • Our ongoing work includes developing multistate survival models to directly estimate transition parameters from aggregate data. Additionally, we are extending the MSM framework to explore various mechanisms of disease processes, including non-progressive tumors and tumors that originate with a high Gleason score. We are also developing methods to incorporate time-varying PSA levels into the MSM framework to investigate PSA-tailored screening strategies.

References

1. Bhatt R, van den Hout A, Pashayan N. A multistate survival model of the natural history of cancer using data from screened and unscreened population. Statistics in Medicine. 2021;40(16):3791-807. [Abstract]
2. Bui MN, van den Hout A, Bhatt R, Pashayan N. Non-homogeneous multistate partial Markov models: A simulation scheme for evaluating cancer screening strategies. Under review.
3. Bhatt R, van den Hout A, Antoniou AC, Shah M, Ficorella L, Steggall E, Easton DF, Pharoah PD, Pashayan N. Estimation of age of onset and progression of breast cancer by absolute risk dependent on polygenic risk score and other risk factors. Cancer. 2024;130(9):1590. [Abstract]
4. Martin RM, Turner EL, Young GJ, Metcalfe C, Walsh EI, Lane JA, Sterne JA, Noble S, Holding P, Ben-Shlomo Y, Williams NJ. Prostate-Specific Antigen Screening and 15-Year Prostate Cancer Mortality: A Secondary Analysis of the CAP Randomized Clinical Trial. JAMA. 2024;331(17):1460. [Abstract]
5. Cuevas Andrade I, van den Hout A, Pashayan N. Parsimonious multistate models using longitudinal data and time-dependent covariates: applications to a liver cirrhosis clinical trial. Under review.
6. Cuevas Andrade I, van den Hout A, Pashayan N. Non-parametric Frailty Model for the Natural History of Prostate Cancer; Using Data from a Screening Trial. In: Einbeck J, Maeng H, Ogundimu E, Perrakis K(eds) Developments in Statistical Modelling. IWSM 2024. Contributions to Statistics. Springer, Cham. Pp 148-152. [Abstract]
7. Cuevas Andrade I, Stavrinides V, Moore C, Emberton M, Giganti F, van den Hout A, Pashayan N. Estimating time to Gleason score progression in MRI-guided active surveillance for prostate cancer. In preparation